
You think computers are so smart, don't you? You use them to look at funny cat gifs, post selfies on Facebook, and think that there's nothing else computers can't do. However, I'm here to tell you that there's a lot computers just can't do. And I'm not talking about things they'll be able to do with more memory or power, it's mathematically proven that computers can never compute these things. But how do you prove a computer literally can't do something? For that, I'm going to need to give a little background.
Note: This is not your average Buzzfeed article. There will be Computer Science and Math. Be warned!!
Introduction:
Have you ever been running a program on your computer when suddenly it seemed like it would take forever to load? At least you think it would take forever to load, maybe if you just let it run for another minute it would finish loading. Wouldn't it be nice to have a way to see if a program was going to halt before running it?
Note: In computer science we treat programs like mathematical functions. Just like if you have f(x) = 3x+2, you can have a computer function/program sendMessage(message,phone_number) which sends a specified message to a specified phone number (the message and phone number being inputs). Just like f(10) = 3*10+2 (32), sendMessage("Hey!", 8002553700) will send the message "Hey!" to the Nintendo Tech Support phone number. This article will use the words function and program interchangeably.
Other note: I'm using a programming language called Python to demonstrate my code (a programming language is simply a way of telling a computer what to do). It reads almost like English, but I'll mark anything not clear with a comment, which will start with a # and will be grayed out. Comments are to be ignored by the computer and read by the human.
If you're already comfortable with functions, feel free to skip to the next section.
Functions:
Most of what computers do is input and output, so it's easy to see why functions are a good model for making computers do things! Back to the problem at hand, it would be really nice to know if a program would halt on an input. It's very easy to reason this about certain programs. Take this program for example:

When you call the function with an input, the computer replaces all instances of 'x' with your specified input. For example, if you told the computer to compute f(10), it would go into the code, and replace the x's with 10s, making this:
return 3*10 + 2
which would be simplified by the computer 32.

With any number as an input (let's use f(10) as an example), this program will definitely terminate. It just plugs in 10 into that equation, and returns the result. There's no stalled processes or anything, so we know for sure that f(x) will halt on input 10. Very trivial.
Take this other function:

This function uses what's called a 'while' loop to achieve what it wants to do. The loop has a statement next to it that is either True or False, and if the statement evaluates to True it continues to do the loop. Looping is something dangerous in terms of halting, and if the statement never becomes False, you'll run into an infinite loop. Here you are safe though, as there are 2 cases (in math we call this proof by cases):
1. If you pass in an odd number, even(x) (with x being the number passed in) will be false, and the make_x_odd will terminate.
2. If you pass in an even number, even(x) will be true, x will get 1 added to it, and then even(x) will be false, making make_x_odd jump out of the loop and terminate.
So we can reason that this function will halt on any integer you give it. QED!

Take this other program:

This is a very malicious program that takes in a message and phone number as input.
The difference between this while loop and the other one is that the statement in this while loop will always be True, as 1+1 will always be equal to 2.
So this program will consistently run the sendMessage program until the computer it's running on is turned off (or someone clicks X). No matter what the input, this program will never halt.
In the 'spam' program the infinite loop is intended, but maybe in another program this could be a mistake. Take this program as an example:

Countdown is a very simple function that seems pretty harmless. I've entered it into my command line and run it for your convenience.
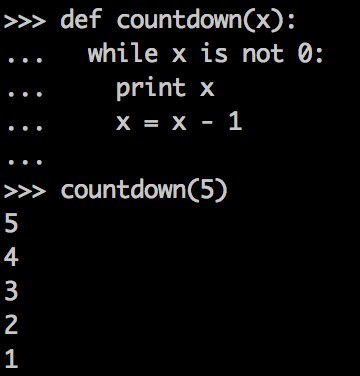
At first this program countdown seems pretty harmless (and useless). It takes in a number as input, and if it's not zero it subtracts 1. This should eventually terminate as x is bound to be equal to 0 at some point, right?
But what if you input a negative number? If you run countdown on a negative number, subtracting 1 from it will never get it to equal 1. So if you ran countdown(1) it would halt very quickly, but running countdown(-1) would leave it running forever.
This program's bug was fairly easy to reason about though, since countdown didn't have much code to it.
Aside: if you want to fix this countdown program, you could change the loop to say "while x>0", which would loop until x>0 was false. If you input a negative number, the loop would never be entered.
Halting
Those were pretty clear examples of when programs will halt and when they won't, but computer programs could get pretty complicated, and it's hard to reason about complicated programs. Here are a few fun stories to get a sense of how complicated these programs can get.
So with infinite loops it would make sense to want to have a way to catch them. If only there was a way to create a program that could analyze other programs and tell you if it halted or not on a given input.
How would we make this function though? We couldn't just run the program on the input and return True if it halts, because then we would have to wait forever to get a "False" result. That's like trying to see if a GIF will ever do something by watching it forever, you'll never know if it eventually will.
We could make a program that waits a certain amount of time, and if it doesn't halt after that amount of time we assume it will never halt. However, this might not work, as maybe if you waited just a LITTLE bit longer it would have halted.
I could keep going, but I'll spoil the surprise. In 1936, Alan Turing (you might have heard of him) proved the Halting problem was uncomputable, that you mathematically cannot have a program that tests if another program will halt on a certain input.
Bummer, right? How could you prove that a computer literally can't do something though? Just because nobody's done it before doesn't mean that it's impossible, right??
Unfortunately, computer scientists can use math to formally prove these things. Guh I hate math.
There's a few ways you can prove this. I'll show you my favorite way, though if you don't follow along there are several videos I'll link to after. This is VERY convoluted, so don't feel bad if you don't understand it on the first try.
It might help to think of the following paradox though: the sentence "This sentence is a lie" is an "uncomputable" sentence the same way the halting problem is undecidable, and here is why!
Assume there is a program defined like this:

halts is a function that given another program and an input, would tell you if that program would halt on that input or not.
For example, if you called halts(f,10) (This is the f that we defined before as 3x+2), it would return true, because f(10) just returns a number and halts.
halts(countdown,10) would return True, but halts(countdown,-10) would return False, since we figured out that negative numbers cause countdown to never halt.
I don't give you code for it because:
a) There is no code, I already told you that it's undecidable
b) We're going to prove halts can't exist because of the effect of what could happen if it did exist
But why can't this function actually exist? (Here's where we start getting tricky)
Assuming halts exists, let's make a new function! (This in math is called Proof by Contradiction - we prove something cannot exist by saying if it did exist crazy things would happen)
Note: If/else statements are pretty self explanatory. If the thing next to the if is true, it runs the code under the if. If the thing next to the if statement is false, it will run the code under the else statement.

This program is a bit confusing, so let me break it down:
trickery takes a program as input, and if that program halts on itself, then trickery will spam that phone number (Nintendo) forever. If the program doesn't halt on itself, then it will do a countdown and then halt. To be more explicit, the program basically does this:

To be EXTRA clear, if the inputted program halts on itself, then trickery will not halt, and vice versa.
So who cares about this dumb function I made? Well here's the thought experiment to kill it all.
What happens if you run trickery(trickery)? Does it halt, or go on forever? Get out a pen and paper, you might need to draw this one out. Here's what happens when you substitute 'program' (the generic name in the function) with 'trickery' (the actual procedure), and maybe you can see the paradox.

The question here is "Does trickery halt on it's own input?"
Let's assume it halts. Well, if trickery(trickery) halts, that means that the if statement had to be false. But the if statement is
"if halts(trickery,trickery)==True"
that trickery halts on trickery! So for trickery to halt on itself, it has to not halt on itself? Contradiction!!
Okay, but maybe trickery(trickery) doesn't halt? For trickery(trickery) to run forever, that if statement needs to be true. But again, the if statement says that trickery halts on trickery! No matter what conclusion we reach, we get a contradiction! What trickery!
So there we have it. All our hopes and dreams of computers that never freeze, crushed by Alan Turing and his mathematics. Damn you Alan Turing!
---
If you enjoyed this (or have any GIF suggestions), please let me know! (and share it and all that other viral stuff). These ideas in computer science and programming really excite me, and I'd like to make them accessible to anyone who is interested in them. I just posted this on Buzzfeed for the meme, but if people show interest I have a ton more I can talk about. You can reach me at arya@brandeis.edu :)
Also GIANT shoutout to all my friends who helped proofread this thing. I love all of you <3

