
Suppose I told you that there are a number of people gathered in a room next door, and that there's better than a 1-in-2 chance that two of them share the same birthday. How many people would you think are in that room?
The number is in fact quite small — just 23.
This is what's known as the birthday problem. More specifically, it refers to the chances that any two people in a given group share a birthday. The reason it is a "problem" is that most people — puzzle lovers and math majors excepted — tend to underestimate its likelihood.
Let's phrase this another way, borrowing an example from this book. You walk into a Las Vegas casino. The blackjack tables are packed, slot machines are buzzing, and in the middle of the room you see an enormous, 365-space wheel of fortune. Someone from the casino calls you over to join a small crowd surrounding the wheel. The casino tells you and the 40 people around you that everyone will take one spin of the wheel. If nobody rolls the same thing, you win. If not, you lose. You take a look around. 365 spots, only 40 other people… seems like great odds.
The problem is that's a losing bet over 90% of the time.
What's striking is that such a small increase of the size of the group can totally skew the odds against you. The odds of beating the casino with a group of 23 people is basically a coin flip, yet upping that number to something not much larger — 41 — makes it horribly skewed. The complete odds look like this:
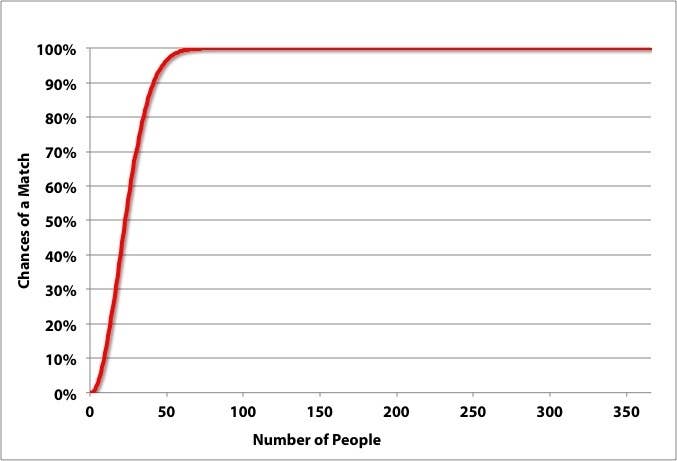
The left side of this chart is what's surprising. In the question I posed at the beginning of this post — in a group of how many people is there a 50-50 chance that two people share a birthday — all the wiggle room is between 0 and 60 people. Any bigger, and it's essentially assured that there is a match, all the way up to 366 people, when it is literally assured.
As math professor Steven Strogatz mentions in this New York Times post, the birthday problem highlights how wrong our intuition can be when it comes to coincidences and chance. We often don't consider the question carefully enough to conceive such a high number of potential birthday matches.
Instead we start comparing how small one number is to the other: "Well… my birthday is Oct. 6… and there are 22 other birthdays in the room… and 22 divided by 365 is pretty small…"
But this question isn't just about you — it's about every person in the room, and the chance that anyone might find a match. The first person in the group has 22 potential birthday matches. The second has 21 (one less because we already counted the first person/second person pair). The third has 20. The fourth has 19. When you add all these up, you get 253 potential birthday pairs.
Maybe because birthdays are so intensely personal, it's easy to turn a question about finding any birthday matches into one about finding my birthday match. It might be why this puzzle is illustrated with birthdays in the first place.
This self-centric intuition — the tendency to turn the question into one about me, or another single person — is exactly what befell Johnny Carson when he gave the birthday problem its most public (mis-)examination on his late-night show in the early '80s. Watch it here:
Mobile link here.
In the video, Johnny Carson and Ed McMahon confuse themselves over the question. Carson remembers the general outline of the problem — something having to do with birthday matches in a small group of people. But after asking two people in the audience for their birthdays and finding no matches in a crowd of 500 people, Carson and McMahon are skeptical about this piece of mathematical trivia.
The issue is that Johnny Carson picked specific birthdays, and thought that he could prove the problem one way or another without checking every person's birthday for a match. He had a huge crowd — 500 people — and once he called on two people who each had unique birthdays in the crowd, just as the video is cutting out, we see that a couple people in the crowd have the same birthday as he does.
This is exactly what we should expect, since in such a large crowd the chance that some pair of people share birthdays is basically 100%. That the first two people had unique birthdays doesn't mean anything — it was just luck, since we wouldn't expect everyone there to share a birthday.
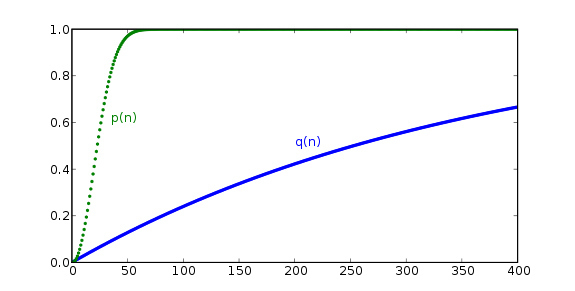
By asking about specific birthday pairs and not about any birthday pairs, Carson confused the particular with the generic. That can make all the difference — look at the gap between the green line and the blue line in the chart above.
Lotteries are a good example of when we correctly distinguish between the particular problem and the generic problem. The odds of you winning the Powerball jackpot are 1-in-175,000,000. Every time someone walks into a drugstore, picks six numbers, and walks out with a winning ticket, this person has made a choice that had 1-in-175,000,000 odds of happening. Yet even though this person is making a 1-in-175,000,000 choice, we're not amazed when someone wins the Powerball. Intuitively we recognize how many millions of people go out and buy tickets and how many opportunities there are for someone to win.
But for the ticket you just bought to be a winner concerns the particular case — the drawing needs to show your six specific numbers. The particular is what's amazing. The generic match — that anyone ever wins the Powerball — isn't.
And that's what the birthday problem is. It's us mistaking the problem as a particular one (where matches are amazing) when it's actually a generic one.
So how does this work out not just in theory but with a real sample? To do something with a little real-world gravitas (at least for my coworkers and I), I gathered the birthdays of 274 other employees at BuzzFeed and took a look.
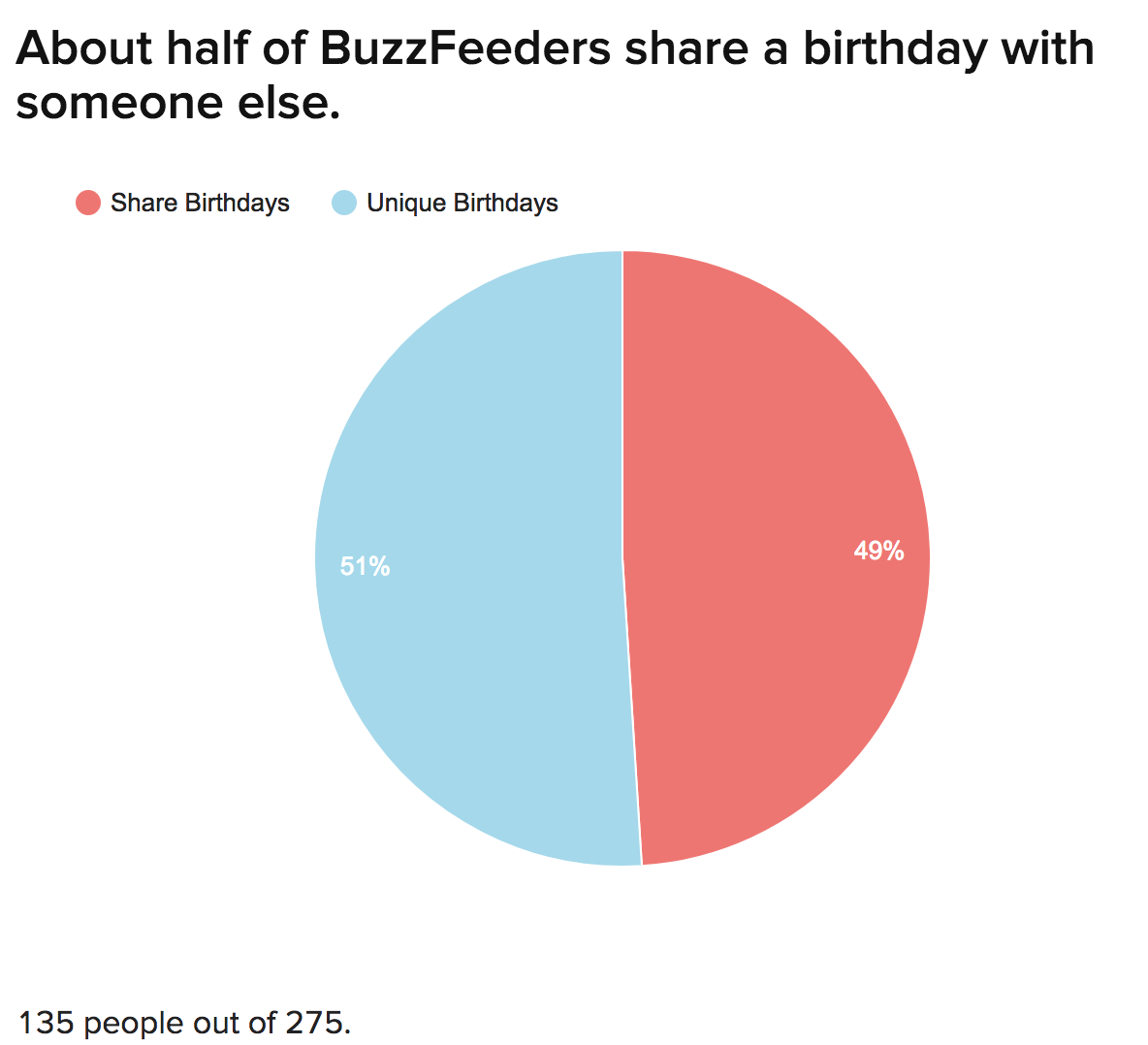
Five people were born on Sept. 9.

Five BuzzFeeders were born on September 9th, an impropable feat even in a group of 275 people — it only becomes more likely than not that five people share a birthday in a group of 313.
